Оптимизационные модели

 
Оптимизационные модели – это модели, предполагающие нахождение экстремума (минимума или максимума) целевой функции (цели оптимизации, при заданной системе ограничений на целевую функцию. Например, целевой функцией может быть максимизацию прибыли предприятия при ограничениях на наличие трудовых ресурсов (материальных, трудовых, финансовых).

 

Пример постановки задачи для торгового предприятия.

 

Торговое предприятие в течение месяца осуществляет продажу товаров n товарных групп, каждая из которых включает r видов товара. На реализацию товара r-го вида каждой j-й товарной группы заданы верхний и нижний пределы товарооборота.

Задача состоит в том, чтобы построить экономико-математическую модель, позволяющую получить оптимальный месячный план продаж по каждому виду товара, обеспечивающий при заданной величине торговой прибыли максимальный объем товарооборота при следующих ограничениях на:

-        площадь торговых залов на единицу товарооборота в натуральном выражении при реализации r-го вида товара из j-й группы;

-        производственную площадь торгового предприятия, м2;

-        месячный фонд времени работы продавцов квалификации l, чел.-ч;

-        норматив товарооборота на группы продавцов квалификации l при реализации r-го вида товара из j-й группы в единицу времени;

-        торговую прибыль от продаж единицы r-го вида товара из j-й группы, ден. ед.;

-        среднюю розничную цену r-го вида товара из j-й группы, ден. ед.;

-        месячный лимит издержек обращения статьи h, ден. ед.;

-        расходы по h-й статье издержек обращения на 1 тыс. ден. ед. товарооборота по реализации r-го вида товара из j-й группы, ден. ед. / тыс. ден. ед.;

-        плановый объем прибыли.

 

 

Оптимизационная задача размещения производства

Экономико-математическая формулировка задачи оптимизации размещения производства в общем виде имеет следующий вид (1) – (4):
 
Задача оптимизации размещения производства
 

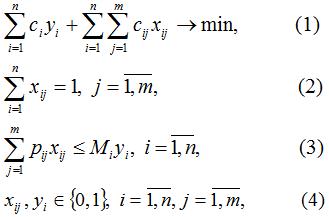
где n – количество возможных пунктов размещения нового производства готовых изделий;

m – количество предприятий-потребителей продукции;

ci (≥ 0)  – стоимость открытия производства в пункте i;

Mi (≥ 0) – максимально возможный объем производства в данном пункте;

cij (≥ 0) – затраты на производство и транспортировку продукции потребителю из региона i в регион j;

xij (≥ 0) – объем продукции i-го предприятия, необходимый для удовлетворения потребностей j-го потребителя;

yi – булева переменная, принимающая значение 1, если i-е предприятие открыто, и 0 – в противном случае;

pij – булева переменная, принимающая значение 1, если i-е предприятие обслуживает j-го потребителя, и 0 – в противном случае.

 

Экономический смысл целевой функции (1) заключается в минимизации суммарных затрат на открытие предприятий и обслуживание потребителей. Ограничение (2) требует удовлетворения потребностей всех потребителей. Неравенство (3) определяет возможность обслуживания потребителей только в открытых предприятиях и ограничивает сверху возможные объемы поставок продукции каждого предприятия.